自然数nの階乗に対する近似式、スターリングの式は漸近的な近似になっている。
つまり、nが大きくなると絶対誤差は拡大する。相対誤差は小さくなる。
100!は厳密には9332621544394415268169923885626670049071596826438162146859296389521759\
9993229915608941463976156518286253697920827223758251185210916864000000\
000000000000000000
指数表現では ![]()
スターリングの式では下記となる
![]()
ザックリ1桁は違っている。でも相対誤差は0.96013程度になるでしょう。
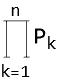
たとえば、
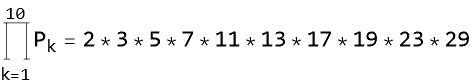
暗中模索して構成した実験式は次ですね。Pn^Pnにこだわった式なわけです。
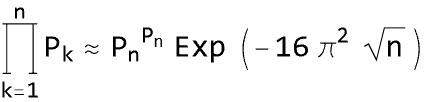
試行錯誤による近似式なので証明もなく、精度も保証されてません。
どのくらい近似できているかを試してみましょう。
![]()
に対して、本実験式は
![]()
とやや小さく評価します。
もっと大きくなると、
![]()
実験式の評価は次の通りです。
![]()
調べてみるとPnの素数階乗の正式な近似式はn^nだとしているようです。スターリングの式との類似性はやや薄いかなと思いますが、チェビシェフの式からの帰結なので裏付けは文句なしです。
実際の値で検討をすると
n=50000では次の値になり、精度はやや落ちる感じです。
![]()
でも、nがもっと大きくなるとこちらが勝つ可能性は高いのでしょうねえ。
【25年12月28日追記】
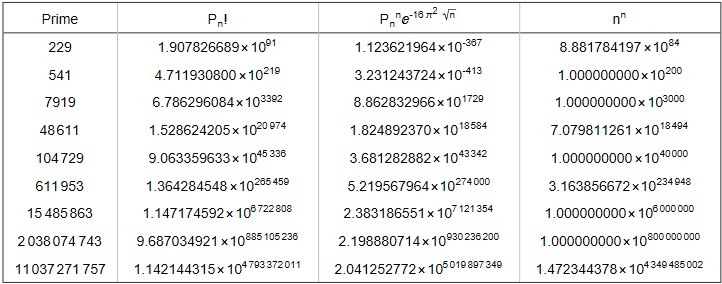
より広範囲で検証を進めてみました。nが5000以上、素数が48611以上になると次の実験式の方がより良い近似となる。
![]()
10^8までの比較結果が下記の表となります。より大きなnではn^nよりも近似度は高いようだ。