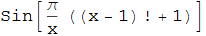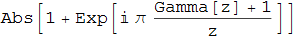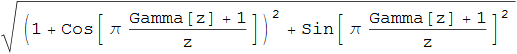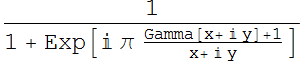素数でゼロになる関数の変種

　ウィルソンの定理を応用した関数である下式はｘが素数で確かにゼロになる。これが数学パズルに引用される関数の変種だ。

なぜなら、（ｐ−１）！＋１はｐが素数のときに限り、ｐで割り切れるからだ。！は階乗記号。
これが、ウィルソンの定理だ。
　よって、ｘが素数であればπの整数倍になるので、サインはゼロになる。
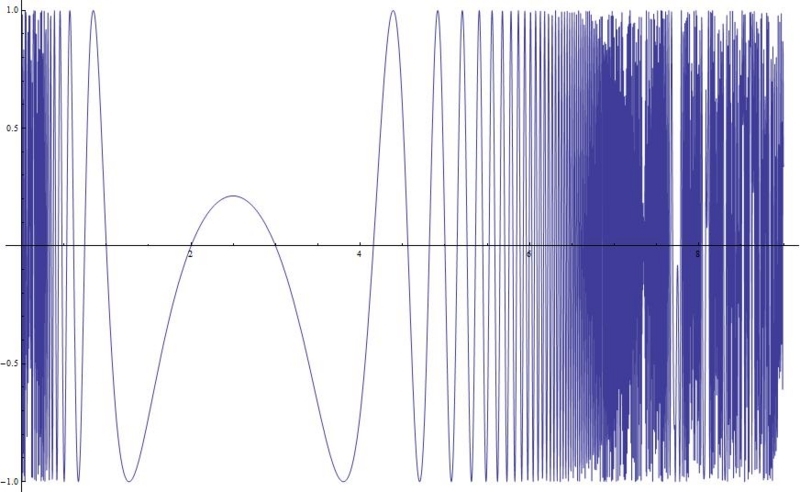
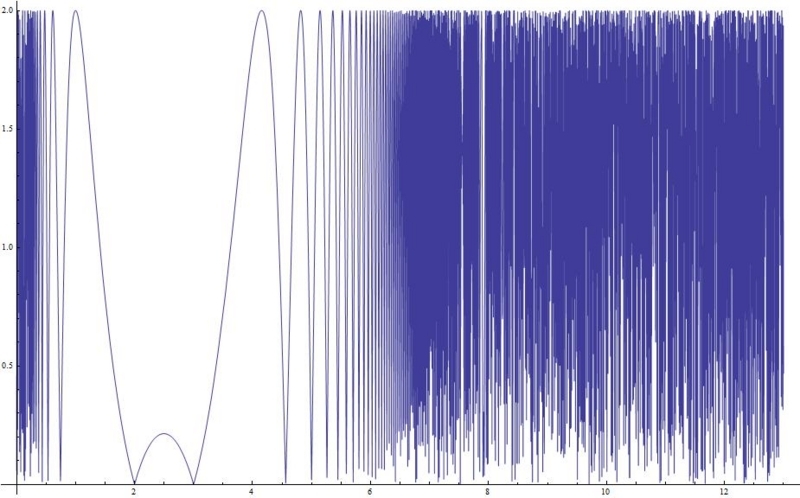
で、グラフを描くとこうなる。確かに２とか３でゼロになっている。

　さればとて、ｘが素数以外の実数値でもゼロになっているということだ。
ここは、素数でしかゼロにならないようにしたい！

　改良を試みる。

　手始めに（ｘ−１）！をガンマ関数Γ（ｘ）に置き換える。諸兄も異論はあるまい。
そのうえで、複素化により書き換えする。Absは絶対値の意味。

これが気に入らない向きには下式に変形してもいいであろう。

というわけで、ｘが正の実数ならば、素数になるときに限り、この関数はゼロになる。ただし、下図のようにガンマ関数の振る舞いがやんちゃ坊主すぎてゼロになるかどうかを追いかけるのは大変だ。

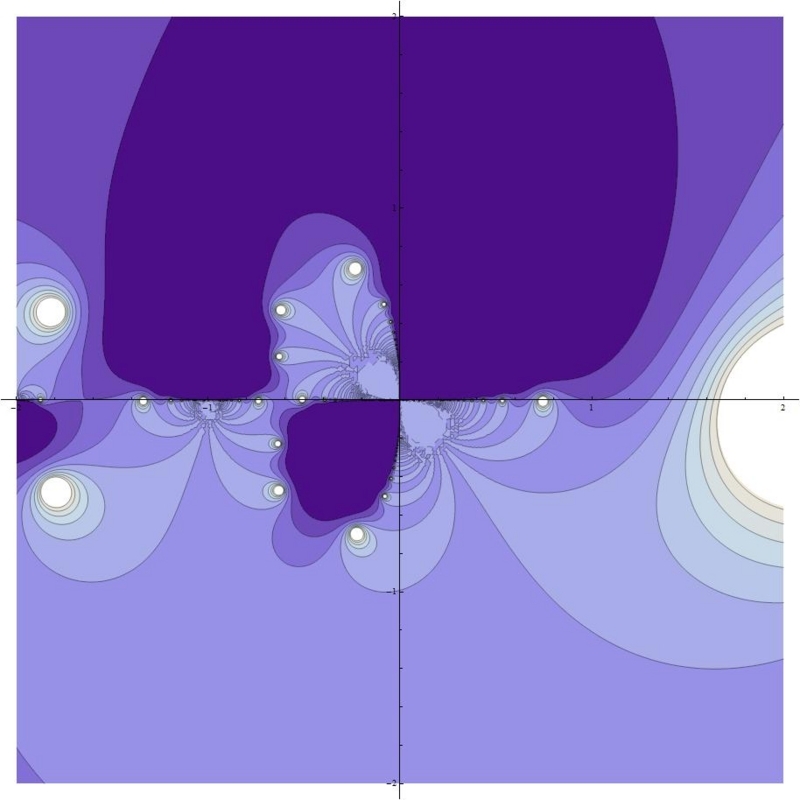
これはという使いみちがない関数であるけれど、素数が極にあるように書き換えて、その挙動を複素平面で描画してみた。実軸は−２と２の間、虚軸も同じ区間で、関数はこうしている。

こうしてビジュアル化するとゼロ点が白く浮き出る。右平面では実軸の素数のみが白くなっているはず（２と３が近いので大きな楕円になっているようだ）。それよりも左平面にゼロ点がいくつか出現していのがおもしろい。

　素数と馴染みのある関数ということで、なんとなく、いい感じの等高線図ではないか。とくに左半平面の渦の出方にワビサビがある。

　流石に欧米の素数オタクも上のような児戯には触れていない。

素数大百科