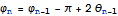円の内部における反射の織りなすパターン

　江戸川乱歩の奇想小説に『鏡地獄』という短編がある。
　レンズや鏡の偏執症の友人が球体鏡を製作する。内側が鏡張りの三次元球で、そこにヒトが入れるようなサイズのものだ。どんな光学的幻像ができるか想像するのはなかなかに難しい。ある人のブログで球面鏡の内部のシミュレーションを報告していたのを数年前に読んだ記憶がある。
下にＹｏｕＴｕｂｅのCGを例示しておきましょう。
　ともあれ、その顛末は当の小説を読んでいただこう。

　ここでは平面の円での慎ましい計算を提示してみる。問題はシンプルだ。
単位円内で周上の点を発した光がどのような軌跡を描くかだ。　でも小細工をしてみる。反射の法則をイジるのである。

　はじめに記号的な概念を説明してみよう。

　Znはｎ番目の反射点である。θnは反射角というわけだ。一般にはθn＝θn+1となる。Φnはｘ軸からの測ったZnへの偏角である。
　Φnについて下式が成立するので、θnの初期値を与えれば、Znは自動的に算出できる。

　結果を図示してみよう。

θn＝π/7で計算する。

　規則性のある星稜が生成された。まずまず、予期した形状である。

外部の円（反射面）を描画してみよう。θn＝π/19

θn＝π/97　　中央にできる円の半径はSinθnとなる。

　反射面に対してθn＝θn+1であるので、規則正しく星形になった。
　それはそれで興味深いが、ビザール＝風変わりさに欠けている感もしないではない。

　よって、この法則をいじりまくるとしよう。反射則を変更するのである。

　思いつきでいい。
　等差数列にしてみよう。
下式は反射のたびに反射角が15度増える。

θn＝θn+1＋π/12

すると、こうなる。　

　非整形ながら乙な形状ではある。

しかし、初期値を変えると同じ反射規則でもこうなる。

　それなら、等比数列の反射則ではどうだろう？

　θn＝2θn+1
初期値がπ/7である。

\[Theta][n_]:= \[Theta][n-1]+Pi/12
初期値がπ/5である。

　すごく他愛のない形状である。
しかしながら、反射則と初期値で大きく光線の軌跡が変化するのは面白い。もう少し、探索してみよう。
　単純な規則で複雑な結果が出る。
　こう云う奴は休日の暇つぶしには最適の計算娯楽ではあるまいか？

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • -

鏡地獄―江戸川乱歩怪奇幻想傑作選 (角川ホラー文庫)