連続的に収縮する三角形模様

　１１月１７日の本ブログでモノした「大した話ではない数の列の生成」が導く結果を説明しましょうか。
　この２４個の数字のセットは、２４個の三角形の中心を計算するための数の組み合わせであります。
オリジナルの三角形の頂点１、頂点２、頂点３の座標をこの順番で足し合わせることを意味しているのですね。

　{{1, 2, 1, 2}, {1, 2, 1, 3}, {1, 2, 3, 1}, {1, 2, 3, 2}, {1, 3, 1, 2}, {1, 3, 1, 3}, {1, 3, 2, 1}, {1, 3, 2, 3}, {2, 1, 2, 1}, {2, 1, 2, 3}, {2, 1, 3, 1}, {2, 1, 3, 2}, {2, 3, 1, 2}, {2, 3, 1, 3}, {2, 3, 2, 1}, {2, 3, 2, 3}, {3, 1, 2, 1}, {3, 1, 2, 3}, {3, 1, 3, 1}, {3, 1, 3, 2}, {3, 2, 1, 2}, {3, 2, 1, 3}, {3, 2, 3, 1}, {3, 2, 3, 2}}

　くだくだしい説明よりは結果をみてもらいましょう。オリジナル三角形を１つ与えます。原点にその中心があります。

　各頂点から子ども三角形が産み落とされます。それはある縮小率でしかも親三角形に相似かつ対称的に配置されてます。オリジナル三角形が正三角形で、５回ほど増殖したケースです。フラクタル的でありますが、どんどん縮小してゆくだけなので単純反復とみなしたほうが良いでしょう。

縮小率を０．９にするとかなり素直な絵柄になりことからもフラクタルとは言い難いと思います。

下図は０．９５です。

三角形を変えることが出来ます。

二等辺三角形を元にしたケースを幾つか。

フラクタルとの違いの一つとしては、オリジナル三角形が隠し絵のように模様のなかに再生していることがあります。
７階層まで反復したケースです。これはあまり美しいとはいえないですね。

むしろこちらの方がいい味出てるかな。

これらは冒頭の数列から生成される次のような複素数の系列から生み出されています。
これが三角形の中心の座標（実数部がｘ、虚数部がｙ）になります。
　なぜ冒頭の数列が必要なのかと申しますと、任意形状の三角形を反転させるためです。言い換えると正三角形だけであるならばこの数列は要らないのあります。

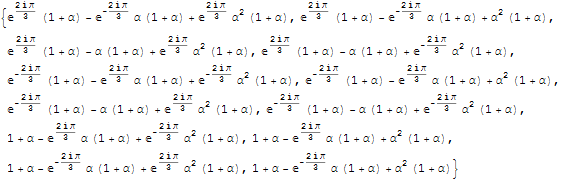
　実はこのやり方は任意の多角形に応用できそうなのであります。追ってレポートしましょうね。
ホンマに複素数は便利ですねえ。

複素数と幾何学