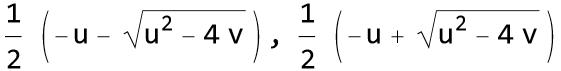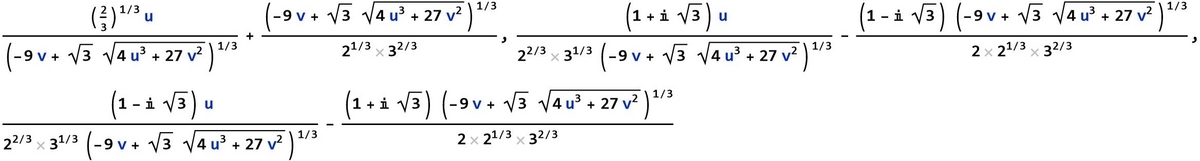前回の続きです。
三次方程式ではカルダーノの解のように2次の項を消去して、解の公式を導出します。
その判別式はこうですね。
四次方程式も同じでした。
実はｎ次方程式もn-1次の項をゼロに変換できます。この操作で方程式の一般性を失いません。これは複素平面で解の総和を原点にシフトしている操作になります。
結果、方程式の簡易化になります。この影響は甚大で、４次方程式までは解の根号による解法が実現するのです。
なので、n-1次の項をゼロにした場合の判別式の項数を出したいというのが、この続報です。
前回は計算限界だった10次方程式の判別式の項数もカウントできました。
1, 1, 2, 6, 19, 76, 320, 1469, 7048, 35233
三次方程式の判別式の項数は２項でカルダーノの解の立方根内のものと一致します。
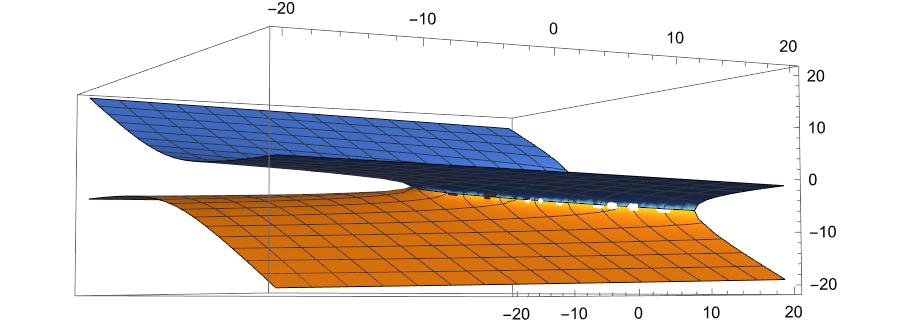
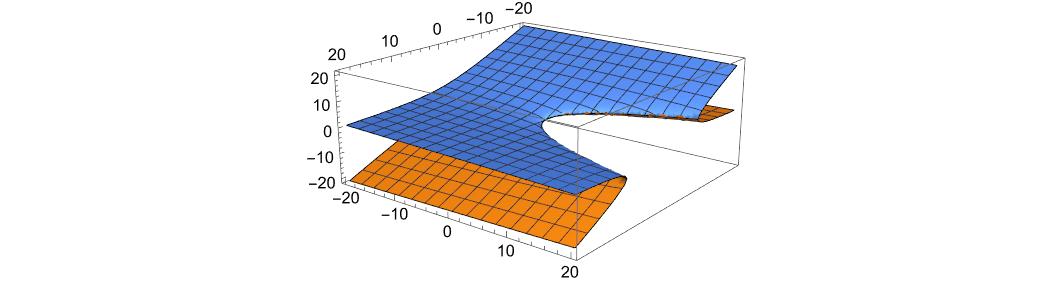
これを対数グラフにしましょう。
前回の結果は９次方程式までで、1, 2, 5, 16, 59, 246, 1103, 5247, 26059でした。
比較グラフです。オレンジの線が今回の結果です。
代数学は方程式の解法の探求だといったとしても大過ないだろう。
義務教育では判別式Discriminantという多項式が二次方程式で重要であることを習う。
次の三次方程式ではどうなるのか？
４次方程式も出しておこう。いずれもn-1次項が縮約されているのは注意しておく。
これが次のような５次方程式でどうなるかを提示しておきます。
判別式の具体な姿はこうなる。５９項ある。
一般的な４次方程式は１６項であり、三次方程式では５項である。二次方程式は２項であったから、半端ない増え方であります。
2,5,16,59,246...... となる。
ここでは9次方程式までの判別式の項数の計算に徹する。
1, 2, 5, 16, 59, 246, 1103, 5247, 26059
まで計算できたが、10次は未達（2時間計算しても）であった。
上記の範囲においても指数関数以上に項数が増大することがわかる。
ところで、この数列はSloan数列プロジェクトに登録されているだろうか？
ありました。
|
2,5,16,59,246までであれば、下記とも一致するそうだ。
| A087949 | G.f. satisfies A(x) = 1 + x*A(x*A(x)). |
【参考文献】
最近になって代数方程式の一般解を鑑みる機会があった。ここでの代数方程式とは、二次方程式、三次方程式、四次方程式のことを指している。
その実の一般解のふるまいをここでは解局面として表示して比較したい。
二次方程式から開始しよう。
この解は義務教育で習ったとおりに下記の2根でありました！
これはuとvの二つの独立変数からなる曲面の式と見なせる。
実（根号内がゼロ以上）ならば、三次元空間で表示できるわけだ。しかも、二つの曲面を同時に描画できる。二葉の曲面がこの実の二つの解に相当するわけだ。
というような2次曲線で接合した曲面になるわけであります。接合線は重根になります。
同様に三次方程式の解は、学校で習った人は知っているように、下の３つの式となる。カルダーノの公式であります。
これも実根が3個あるという条件であるなら、三次元空間に一挙に描画できる。
三個の曲面が接合している。
三枚の曲面が原点あたりで接した配置になっている。u,vの第２象限あたりは三枚が重なるようだ。接合部は重根の集合だけれど、二重根と三重根の場合があるので、多少入り組んだ線になる。
たぶん、面上の白い線は特異点の集合で三次曲線になっているのだろう（ほんとかな？）また、白線より右側は３実根がある領域でもある（判別式が正）
しまいに、四次方程式だ。一般性を欠いている。二次と三次の項を略したので。
この4つの解を計算するのだが、根の式は一つだけ下に表示する。
この4つの曲面を例示しておきます。見ての通り、実の2根までで同時に実の4根は存在しないようである。
これらはいずれも、-20<u<20 -20<v<20 での計算結果でありました。
四次方程式に関してだけ、つけたし計算をしておきます。
このパターンで3次の項を追加したケースの曲面です。
上記の整然とした曲面のつながりが複雑な接合に変容しているのが見て取れます・
グレーゾーンは計算不可域です。2番目のビューでは4実根の存在がうかがわれます。
【参考文献】
Hardy Littlewoodの定数という双子素数の拡張に関する定数がある。
ここでｐはｎ以上のすべての素数であり、無限個での積の極限を意味する。n=6とする
自分の非力な計算機と能力では、素数を2000000個まででの計算しかできなくて
その値は0.186614302085344364095,,,,,,,,,,となる。
だが、如何なる偶然の仕業か！ 下のような三角関数の積の極限値が異様に近い。
この近似値は0.186611388026708605231894491738........となる。
両方とも数学的なバックグラウンドは別物だということは注意しておく。
どうやら一致は小数点5桁までなのだが、ここまで近いケースは始めての遭遇。
流体力学では複素関数Fを二次元にける流れ（非圧縮流体）のモデルとみなす。複素ポテンシャルとも呼びます。
とくにFを実部と虚部に分けて、虚部Ψを流れ関数という。
F(z)=Φ(x,y)+iΨ(x,y)
虚部Ψ＝一定の等高線は流線という。流れを表す線というわけであります。
これを孤立特異点に適用してみます。
いつものように f(z)=Exp(1/z) を対象にします。比較のためにg(z)=1/(1-z)も扱いましょう。
そして、いきなりf , g を計算する前に有限級数の原点付近（z=0）での展開を逐次的に図式化します。多くの極を重ねていくと孤立特異的になるわけである。
それぞれｍを極限まで大きくすれば、f(z)=Exp(1/z) とg(z)=1/(1-z)になる。
例えば、ｍ＝２として、ｘとｙが-1/2と1/2の間で流線の等高線図をそれぞれ描く。
上がｆ2, 下がg2である。
あまり差がないようだ。しかし、m=10になると対称性が違ってくる。
これらをそれぞれ動画にしてみた。ｍが１から40までの連続描画であります。
因みに、今井功の流体数学（下の参考文献）によれば極は湧き出しと吸い込みが合体したと解釈できる。
例えば1/z^2はダイポール（双極子）というものに相当する。こうした多重特異点を重ね合わせたものが孤立特異点になるようなのだ。
ｆのケース
ｇのケース
ｆをもう少し拡大した範囲（-1/10から1/10）できめ細かく計算してみよう。
【参考文献】
かつて学部時代にお世話なった古典。
複素関数論を流体力学的に逆写像した珍しい本でありました。物理屋には有難い本
ｎ項の基本対称式のパターンがｎ個あるという前回の話の継続であります。
すなわち、5個の変数があれば、
次のような5個の基本対称式の種類がある。
今回はこれを自然数に対して適用して、素数の出現を表現するという面白半分の試みです。
例えば、自然数1,2,3,4,5に対して、基本対称式の5種の計算値は15, 85, 225, 274, 120となる。ここでの素数は皆無である。
n=１から10までにこれを繰り返す、個々の素数判定を可視化してみよう。パスカルの三角形的に表示してみた。
白抜き四角が素数であり、黒は合成数である。素数は少ないですね。
これを（基本対称式+1）で試行しよう。n=5での実例は16, 86, 226, 275, 121だ。
n=１から30までにこれを繰り返す、それらの素数判定結果を表示しよう。
かなり素数の頻度は増加する。であるけれど。目立った規則性はないようだ。
右隅の□は n!+1が素数になるケースだ。
これだけでも計算時間は1時間かかった。
ほかに素数が頻出するのは、偶数列からの基本対称式だろうか。
つまり、{2, 4, 6, 8, 10}の5個の連続偶数から、{30, 340, 1800, 4384, 3840}が生成され、それぞれに１を加算して、{31, 341, 1801, 4385, 3841}が生まれる。
一番目と三番目が素数になる。これをn=30まで計算したのが下図である。
一番目の基本対称式（単純和）は14回素数になっている。
打率5割に近いので、大谷翔平も顔負けであります。
