最近になって代数方程式の一般解を鑑みる機会があった。ここでの代数方程式とは、二次方程式、三次方程式、四次方程式のことを指している。
その実の一般解のふるまいをここでは解局面として表示して比較したい。
二次方程式から開始しよう。
![]()
この解は義務教育で習ったとおりに下記の2根でありました!
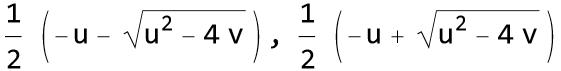
これはuとvの二つの独立変数からなる曲面の式と見なせる。
実(根号内がゼロ以上)ならば、三次元空間で表示できるわけだ。しかも、二つの曲面を同時に描画できる。二葉の曲面がこの実の二つの解に相当するわけだ。
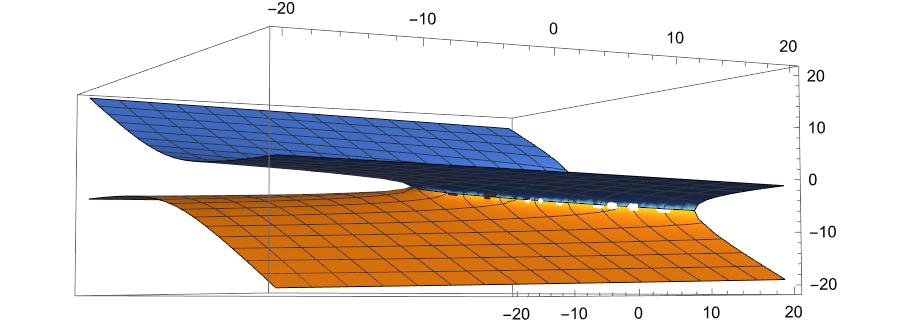
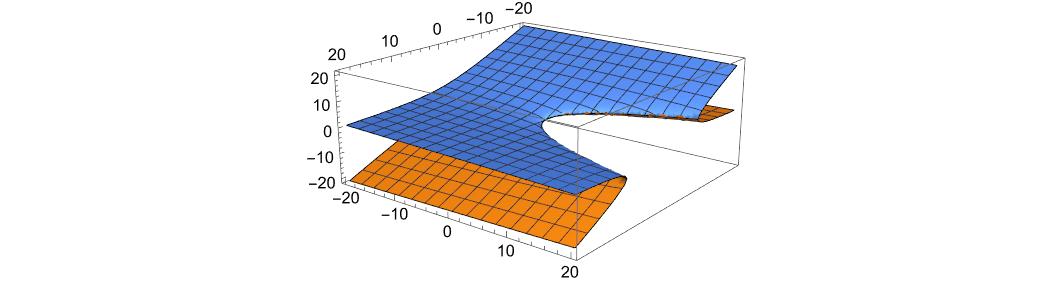
というような2次曲線で接合した曲面になるわけであります。接合線は重根になります。
同様に三次方程式の解は、学校で習った人は知っているように、下の3つの式となる。カルダーノの公式であります。
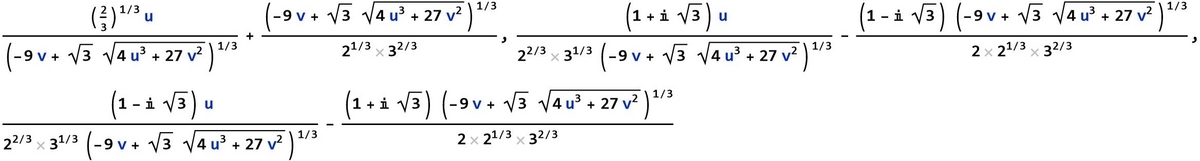
これも実根が3個あるという条件であるなら、三次元空間に一挙に描画できる。
三個の曲面が接合している。
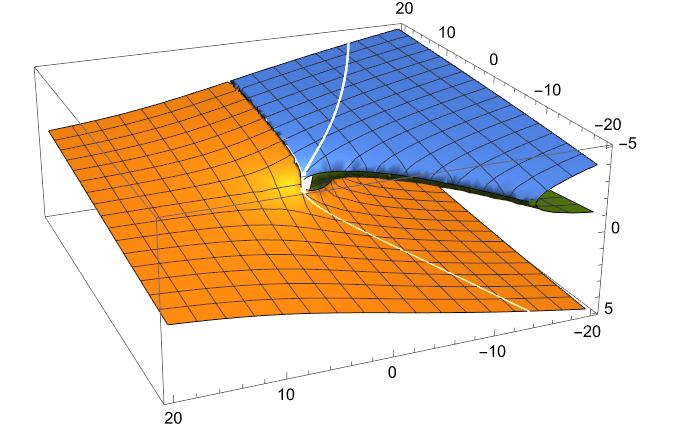
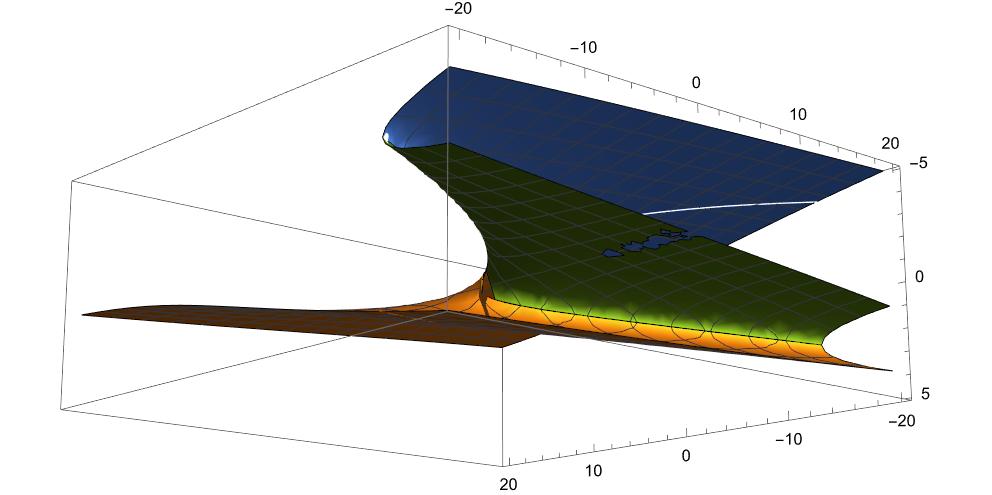
三枚の曲面が原点あたりで接した配置になっている。u,vの第2象限あたりは三枚が重なるようだ。接合部は重根の集合だけれど、二重根と三重根の場合があるので、多少入り組んだ線になる。
たぶん、面上の白い線は特異点の集合で三次曲線になっているのだろう(ほんとかな?)また、白線より右側は3実根がある領域でもある(判別式が正)
しまいに、四次方程式だ。一般性を欠いている。二次と三次の項を略したので。
![]()
この4つの解を計算するのだが、根の式は一つだけ下に表示する。
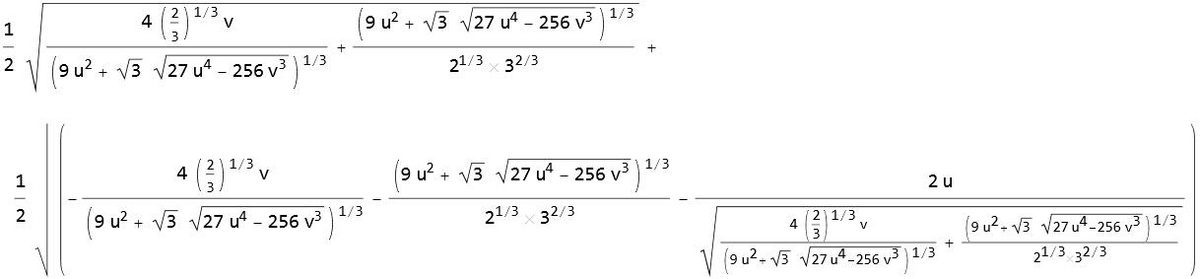
この4つの曲面を例示しておきます。見ての通り、実の2根までで同時に実の4根は存在しないようである。
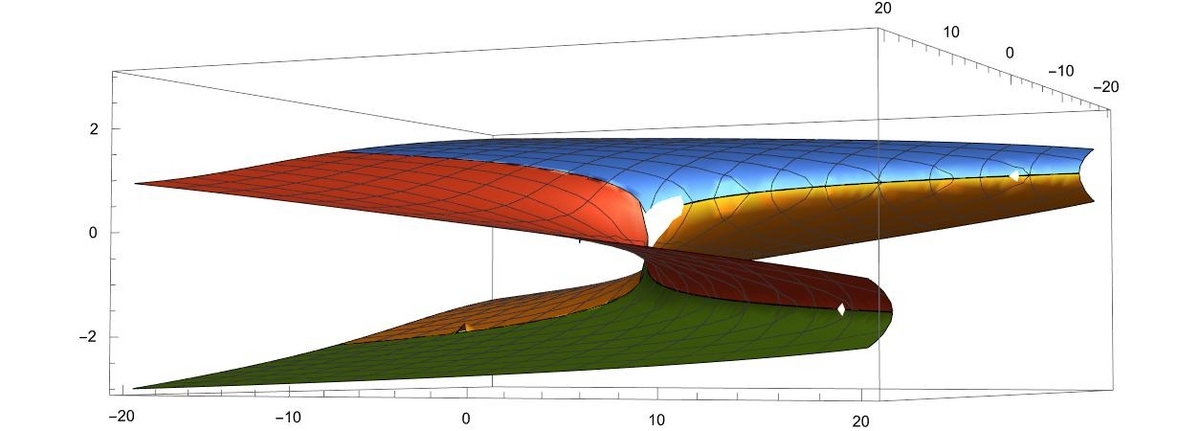
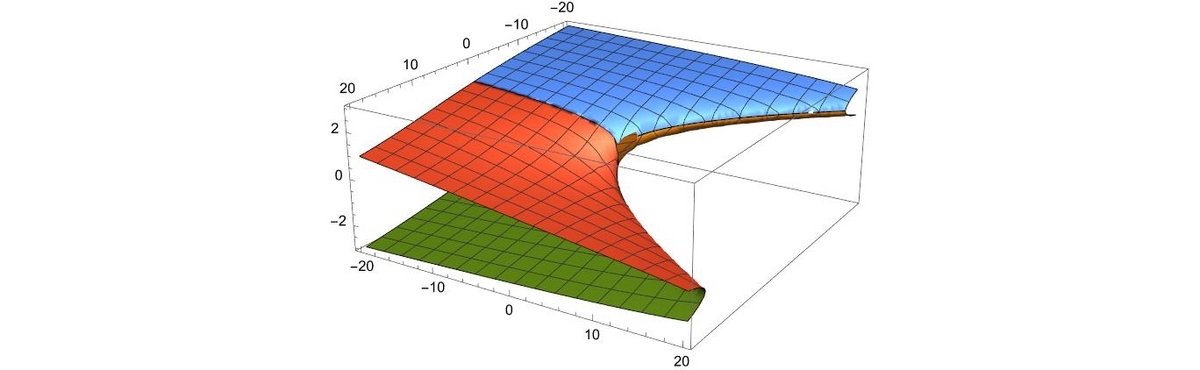
これらはいずれも、-20<u<20 -20<v<20 での計算結果でありました。
四次方程式に関してだけ、つけたし計算をしておきます。
このパターンで3次の項を追加したケースの曲面です。
![]()
上記の整然とした曲面のつながりが複雑な接合に変容しているのが見て取れます・
グレーゾーンは計算不可域です。2番目のビューでは4実根の存在がうかがわれます。
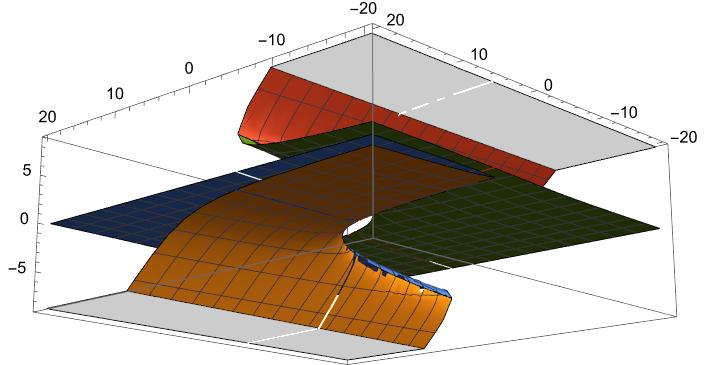
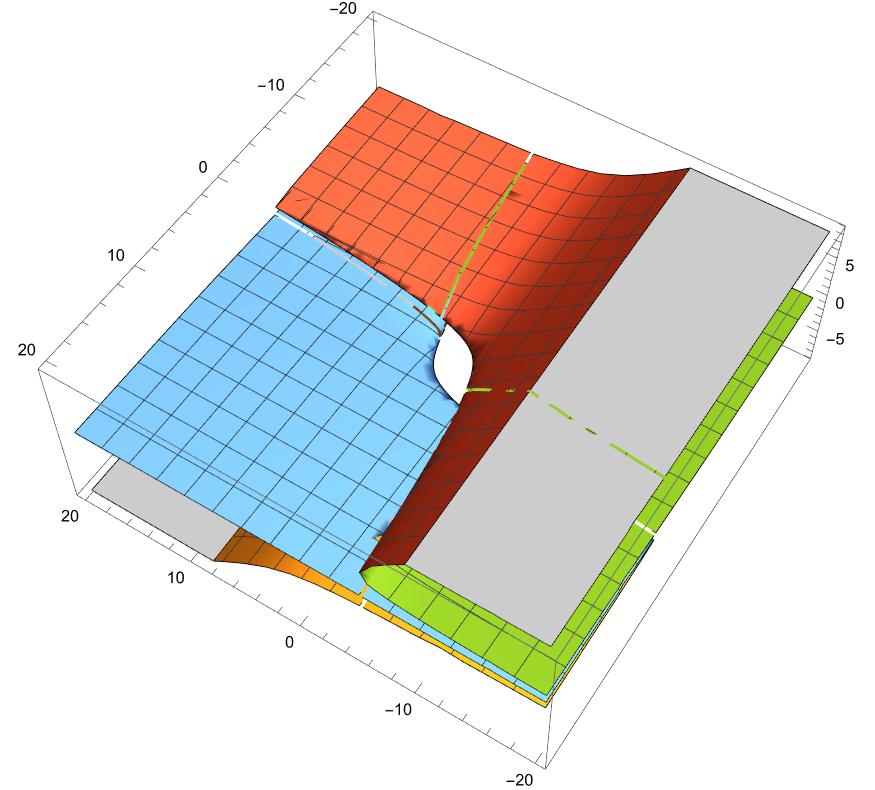
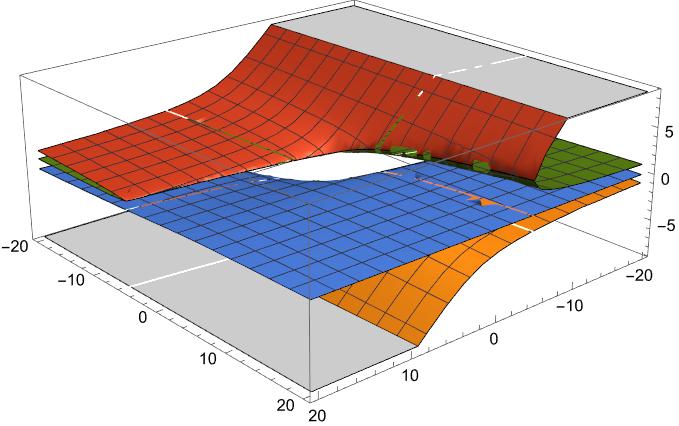
【参考文献】
