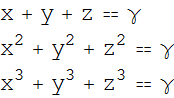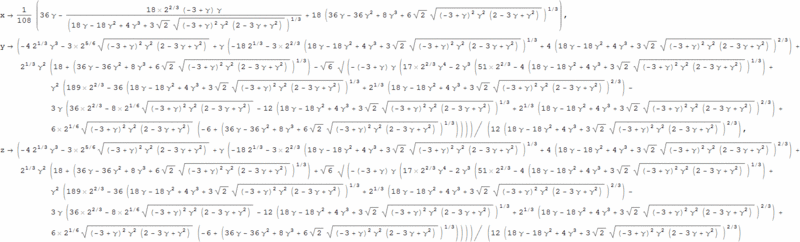対称式の連立三元三次方程式のある種のものの解

　x,y,zについての連立方程式を考える。γは所与とする。

解は存在する。三次方程式なので可解なのであります。厳密解まで求められる。
その一つはこんな有り様です。

通常ではここでオシマイ、なのであるけれど、この連立方程式は３次元空間内の曲面であった。
平面と球面と三次曲面の交わる点が「解」であるはずだ。もちろん、実解のみだ。複素数は表現できないのだから。
　例えばの話、γ＝２ならば、どうなるだろうか？

　手始めに、三次曲面を表示しておこう。

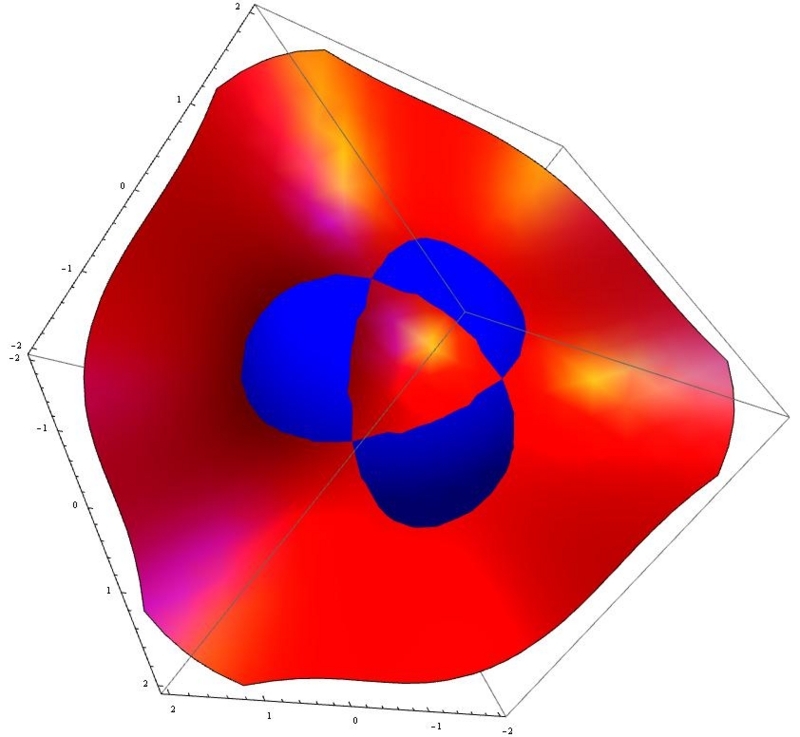
　球面を重ねる。いずれもγは２としている。

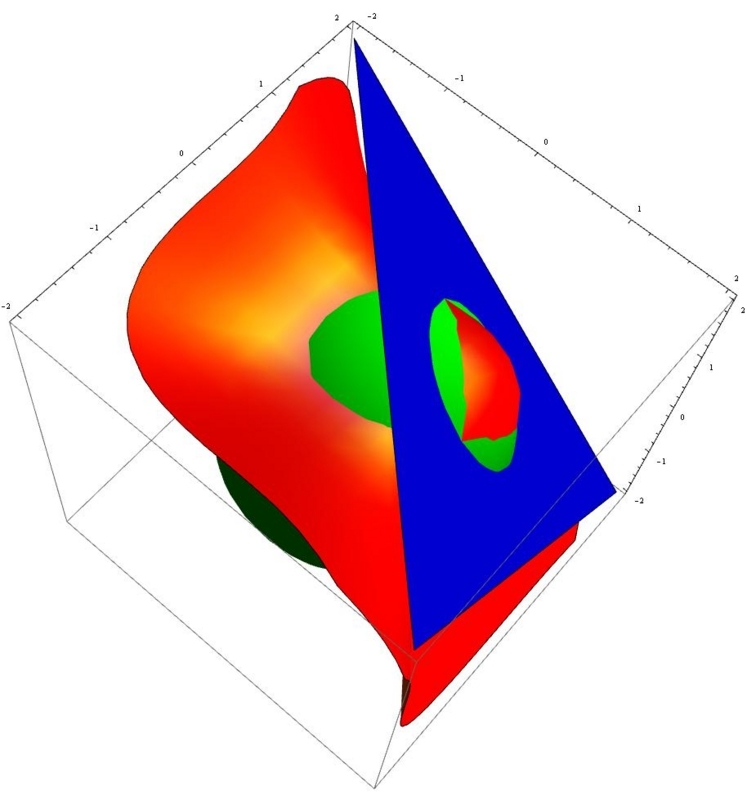
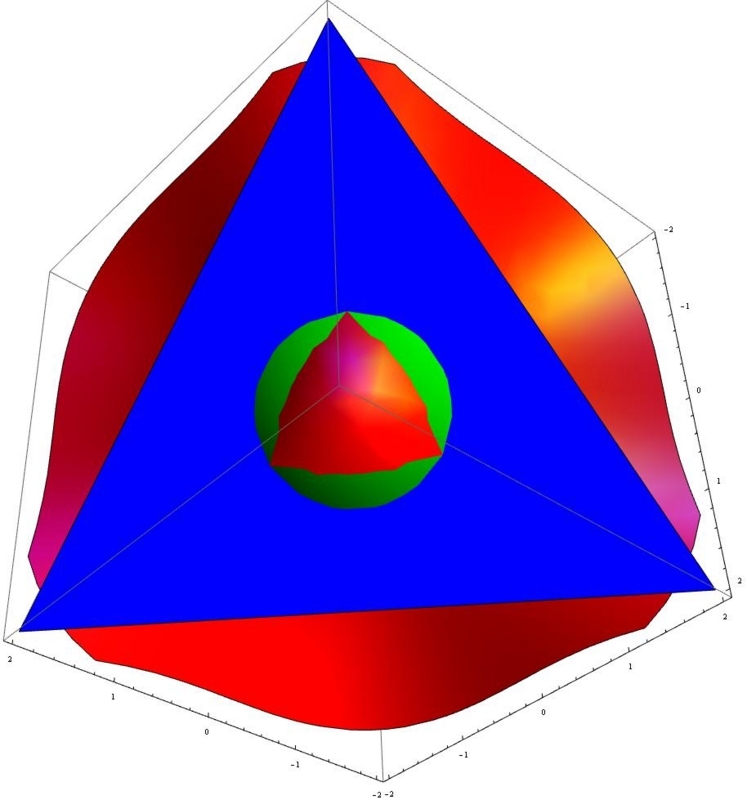
赤が三次曲面で青が球面だ。これに平面を重ねたものが下図だ。

回転させてみると三角形の頂点が解であるらしい。赤と青と緑の３個の接点である。

逆にいうならば、そう、実の解がありそうなわけであります。上の厳密解の式にγ＝１を代入するとこうなる。

　変形が必要な複雑な数値解にみえるかもしれない。
　でも、深く考えるまでもなく、上の図の三交点は(1,1,0),(0,1,1),(1,0,1)なのでありました。
しかし、γがいかなる範囲にあるときに解（実数）があるのであろうか。

【参考資料】

　最近は曲面なんて単純すぎて誰も研究していないのかもしれませんねえ。この本は昔、図書館で借りたけど図が多くて楽しかった。