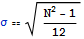自然数と素数の統計的特性の比較 - 完全無欠で荒唐無稽な夢

　数論学者たちの絶対しないこと、禁じ手は素数を統計的集団として扱うことだろう。規則性がある集合に対して、あの立場の違う＝練度の低い記述統計学を適用するなどはお門違いというわけである。
　素人的にはそれは関係ない。
　なので、以下はまったくの興味本位の試行である。

１からNまでの自然数の集合とその中の素数の集合の基礎統計量を計算してみよう。
平均値と標準偏差を計算するのだ。

　自然数の集団では、平均値＝（Ｎ＋１）/2　である。標準偏差σはこうなる。

　N以下の素数の集合についてはこのような簡易化表現はできない。

ちなみにN=100までの平均値を比較する。

　自然数集合の平均値＝50.5　　　　素数集合の平均値=42.4
　自然数集合のσ＝29.0115　　　　素数集合のσ=29.476

ざっと見、素数の平均値は小さめで、標準偏差は大きい傾向になるのであろう。

　素数集合の平均値/自然数集合の平均値をNの関数でプロットしてみよう。

　この極限値は「１」になるのであろう。

N=1000000では「0.956722」であった。

　σについてはどうだろうか？

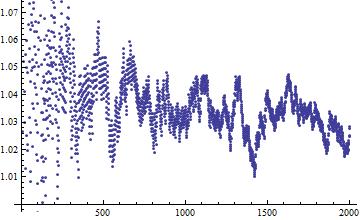
素数集合のσ/自然数集合のσをNの関数でプロットした。N=1000までの範囲だ。

　
　素数集合のほうが散らばりが大きいというのはわかる。
されにCV（変動係数）で考えてみよう。

　変動係数はσ/平均値で定義される。一様分布では「０」となる。ポアソン分布では「１」になる。これも一種の散らばり方を示すのだが、自然数集合ではその極限値は

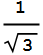
に近づくことが簡単に証明できる。
　その値は0.57735026918962576450914878050196．．．である。

素数集合ではそう簡単ではないので、数値計算しかない。
素数の変動係数のN＝10000（それ以下の素数集合）までの計算結果だ。

　この数は収束するのだろうが、極めて遅い。N=8000000まででは「0.5834922172」だが、それでも収束してない。自然数集合よりやや大きい。これは何らかの超越数になるだろう、たぶん。

　どなたか精度の高い計算してみないだろうか。

【追記】
N=100000000まででCV＝0.601935810101041248981397256739
N=200000000まででCV＝0.600882601205654322262673894226になる。
　ひょっとしたら「0.6」なのか？

素数マニア学者の専門書にも上記の計算は含まれない。常軌を逸した素数の記述統計というわけだ。